En el Trabajo Practico de los Numero Reales vimos su clasificación de la misma.
- Números Naturales: Con los números naturales contamos los elementos de un conjunto (número cardinal). O bien expresamos la posición u orden que ocupa un elemento en un conjunto (ordinal).
El conjunto de los números naturales está formado por:
N= {0, 1, 2, 3, 4, 5, 6, 7, 8, 9,...}
- Números Enteros: Nos permiten expresar: el dinero adeudado, la temperatura bajo cero, las profundidades con respecto al nivel del mar, etc.
 = {...−5, −4, −3, −2, −1, 0, 1, 2, 3, 4, 5 ...}
= {...−5, −4, −3, −2, −1, 0, 1, 2, 3, 4, 5 ...}
- Números Racionales: Se llama número racional a todo número que puede representarse como el cociente de dos enteros, con denominador distinto de cero.Se llama número racional a todo número que puede representarse como el cociente de dos enteros, con denominador distinto de cero.

- Números Irracionales: Un número es irracional si posee infinitas cifras decimales no periódicas, por tanto no se pueden expresar en forma de fracción.
 = 3.141592653589...
= 3.141592653589...
Número de Oro
Un número nada fácil de imaginar que convive con la humanidad porque aparece en la naturaleza y desde la época griega hasta nuestros días en el arte y el diseño. Es el llamado número de oro (representado habitualmente con la letra griega ) o también sección áurea, proporción áurea o razón áurea
) o también sección áurea, proporción áurea o razón áurea
Número Pi
TRABAJO PRACTICO N°2: Función Lineal
En geometría y el álgebra elemental, una función lineal es una función polinómica de primer grado; es decir, una función cuya representación en el plano cartesiano es una linea recta. Esta función se puede escribir como:
TRABAJO PRACTICO N°3: Estadística
Gráficos:
La finalidad de los gráficos estadísticos es que la información entre por los ojos. Los hay de
muy diversos tipos, pero todos ellos resultan muy fáciles de interpretar, pues esa es,
precisamente su razón de ser.
¿Cómo se clasifican y usan los gráficos?
Gráficos lineales
Se usan habitualmente para representar serie cronológicas, cuando se tienen más de siete
categorías.
Se representan ciclos por ejemplo de enero a diciembre.
Se construyen marcando cada valor de la serie de tiempo en el eje de las abscisas. La otra
variable se representa en el eje de las ordenadas. Luego de consignados todos lo puntos en
el cuadrante del gráfico se procede a unirlos por una raya de tal modo que queda construida
una línea quebrada que permite visualizar el seguimiento de una variable a través del
tiempo.


Gráficos de Barras
Consiste en representar mediante líneas o barras separadas la magnitud de las frecuencias
referidas a una escala. Son particularmente útiles para comparar datos provenientes de
serie cualitativas o cuantitativas discretas. Hay algunas consideraciones que deben ser
tenidas en cuenta en este tipo de gráficos:
Sectogramas
Se usan para representar la distribución de frecuencias de una serie cuanti o cualitativa o
para expresar porcentajes. El total de las observaciones o el 100% corresponden al total del
círculo, y la frecuencia o porcentaje de cada clase se representa mediante el sector cuyo
ángulo central es proporcional a la magnitud de la clase. Se usa la regla de tres simple.
Este gráfico se recomienda cuando se desean representar pocas categorías.
Pictogramas
Para este tipo de gráficos se selecciona un dibujo de manera que sugiera la naturaleza de
los datos que se presenta. A esta figura se le asigna un valor en las unidades que esta
representa y se repite tantas veces en le gráfico hasta alcanzar la magnitud del fenómeno.
Al confeccionar estos gráficos se deben tener en cuenta que las cantidades mayores se
indican por un número mayor de símbolos no por símbolos más grandes.
Tablas y Gráficos Estadísticos
Tablas
Las tablas estadísticas aparecen por todas partes y consisten en masas
estructuradas de datos. Con frecuencia su aspecto es temible y al no experto le
producen la sensación de que poco o nada podrá sacar en claro de ellas. Sin
embargo si se las mira con fe se puede apreciar que no sólo no es difícil, sino que es
muy fácil leer en ellas.
Pero si además de con fe, se las mira con un poco de conocimiento, los datos
cobran vida y dirán mucho más de lo que puede aparecer a primera vista.
Reflexionemos
Las tablas estadísticas están confeccionadas de tal modo que resultan muy
fáciles de leer y de interpretar. Utiliza fundamentalmente el sentido común.
Las tablas estadísticas tienen mucha más información que la que aparece a
primera vista. Para obtenerla conviene relacionar unas líneas con otras,
operar con ellas, obtener conclusiones adicionales. Para ello se debe recurrir
con frecuencia a la interpretación como porcentajes de uno datos respecto de
otros.
En todas las tablas suele haber redundancias, es decir, se da información que
podía haberse obtenido por otro conducto dentro de la misma tabla. Esto es
lógico, pues la misión de una tabla no es sólo dar información, sino facilitar la
lectura de la misma.
Es muy frecuente, que las tablas que vienen en diarios, revistas, libros de
divulgación, folletos informativos, etc., tengan errores. (hasta tal punto que
estamos tentados a dar una regla que diga: toda tabla tiene errores, con la
convicción de que la regla tendrá muy pocas excepciones). Las redundancias
permiten descubrirlos. También el sentido común y nuestros conocimientos
previos nos alertan, a veces, sobre datos chocantes: en tal caso recurre a
otras fuentes.
Estadística Descriptiva
La estadística descriptiva es una gran parte de la estadística que se dedica a recolectar, ordenar, analizar y representar a un conjunto de datos, con el fin de describir apropiadamente las características de este.
A partir del siglo XIX , entre otros, con el aporte de Adolphe Quetelet (1796-1874), se crearon diferentes métodos de cálculo de probabilidades para determinar y analizar el tipo de datos que regulan algunos fenómenos.
Media Aritmética: Se obtiene a partir de la suma de todos sus valores dividida entre el número de sumados.
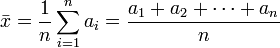
a) Si n es impar, la mediana es el valor que ocupa la posición una vez que los datos han sido ordenados (en orden creciente o decreciente), porque éste es el valor central.
una vez que los datos han sido ordenados (en orden creciente o decreciente), porque éste es el valor central.
El número irracional más conocido es  , que se define como la relación entre la longitud de la circunferencia y su diámetro.
, que se define como la relación entre la longitud de la circunferencia y su diámetro.
 , que se define como la relación entre la longitud de la circunferencia y su diámetro.
, que se define como la relación entre la longitud de la circunferencia y su diámetro. = 3.141592653589...
= 3.141592653589...
Otros números irracionales son:
El número e aparece en procesos de crecimiento, en la desintegración radiactiva, en la fórmula de la catenaria, que es la curva que podemos apreciar en los tendidos eléctricos.
e = 2.718281828459...
El número áureo,  , utilizado por artistas de todas las épocas (Fidias, Leonardo da Vinci, Alberto Durero, Dalí,..) en las proporciones de sus de sus obras.
, utilizado por artistas de todas las épocas (Fidias, Leonardo da Vinci, Alberto Durero, Dalí,..) en las proporciones de sus de sus obras.
 , utilizado por artistas de todas las épocas (Fidias, Leonardo da Vinci, Alberto Durero, Dalí,..) en las proporciones de sus de sus obras.
, utilizado por artistas de todas las épocas (Fidias, Leonardo da Vinci, Alberto Durero, Dalí,..) en las proporciones de sus de sus obras.Número de Oro
Un número nada fácil de imaginar que convive con la humanidad porque aparece en la naturaleza y desde la época griega hasta nuestros días en el arte y el diseño. Es el llamado número de oro (representado habitualmente con la letra griega
Número Pi
π (pi) es la relación entre la longitud de una circunferencia y su diámetro, en geometría euclidiana. Es un número irracional y una de las constantes matemáticas más importantes. Se emplea frecuentemente en matemáticas, física e ingeniería. El valor numérico de π, truncado a sus primeras cifras, es el siguiente:
El valor de π se ha obtenido con diversas aproximaciones a lo largo de la historia, siendo una de las constantes matemáticas que más aparece en las ecuaciones de la física, junto con el número e. Cabe destacar que el cociente entre la longitud de cualquier circunferencia y la de su diámetro no es constante en geometrías no euclidianas.
TRABAJO PRACTICO N°2: Función Lineal
En geometría y el álgebra elemental, una función lineal es una función polinómica de primer grado; es decir, una función cuya representación en el plano cartesiano es una linea recta. Esta función se puede escribir como:
donde m y b son constantes reales y x es una variable real. La constante m es la pendiente de la recta, y b es el punto de corte de la recta con el eje y. Si se modifican entonces se modifica la inclinación de la recta, y si se modifica b, entonces la línea se desplazará hacia arriba o hacia abajo.
Algunos autores llaman función lineal a aquella con b = 0 de la forma:
mientras que llaman función afín a la que tiene la forma:
cuando b es distinto de cero, dado que la primera (b = 0) es un ejemplo también de transformación lineal, en el contexto de álgebra lineal.
f(x) = mx + b
f(x) = mx
f(x) = mx + b
f(x) = mx + b
f(x) = mx
f(x) = mx + b
TRABAJO PRACTICO N°3: Estadística
Gráficos:
La finalidad de los gráficos estadísticos es que la información entre por los ojos. Los hay de
muy diversos tipos, pero todos ellos resultan muy fáciles de interpretar, pues esa es,
precisamente su razón de ser.
¿Cómo se clasifican y usan los gráficos?
Gráficos lineales
Se usan habitualmente para representar serie cronológicas, cuando se tienen más de siete
categorías.
Se representan ciclos por ejemplo de enero a diciembre.
Se construyen marcando cada valor de la serie de tiempo en el eje de las abscisas. La otra
variable se representa en el eje de las ordenadas. Luego de consignados todos lo puntos en
el cuadrante del gráfico se procede a unirlos por una raya de tal modo que queda construida
una línea quebrada que permite visualizar el seguimiento de una variable a través del
tiempo.


Gráficos de Barras
Consiste en representar mediante líneas o barras separadas la magnitud de las frecuencias
referidas a una escala. Son particularmente útiles para comparar datos provenientes de
serie cualitativas o cuantitativas discretas. Hay algunas consideraciones que deben ser
tenidas en cuenta en este tipo de gráficos:
-Gráficos de barras verticales
Los Gráficos de barras verticales representan valores usando trazos verticales, aislados o no unos de otros, según la variable a graficar sea discreta o continua. Pueden usarse para representar una o más series
-Gráficos de barras horizontales
Los Gráficos de barras horizontales representan valores discretos a base de trazos horizontales, aislados unos de otros. Se utilizan cuando los textos correspondientes a cada categoría son muy extensos. Pueden usarse para representar una o más series.
-Gráficos de barras proporcionales
Los Gráficos de barras proporcionales se usan cuando lo que se busca es resaltar la representación de los porcentajes de los datos que componen un total. Dichas barras pueden ser verticales u horizontales.
-Gráficos de barras comparativas
Los Gráficos de barras comparativas son las mismas barras ya utilizadas que pueden utilizarse para comparar dos o más series, para comparar valores entre categorías.
-Gráficos de barras apiladas
Los Gráficos de barras apiladas se usan para mostrar las relaciones entre dos o más series con el total. Las barras también pueden ser verticales u horizontales.
Se usan para representar la distribución de frecuencias de una serie cuanti o cualitativa o
para expresar porcentajes. El total de las observaciones o el 100% corresponden al total del
círculo, y la frecuencia o porcentaje de cada clase se representa mediante el sector cuyo
ángulo central es proporcional a la magnitud de la clase. Se usa la regla de tres simple.
Este gráfico se recomienda cuando se desean representar pocas categorías.
Pictogramas
Para este tipo de gráficos se selecciona un dibujo de manera que sugiera la naturaleza de
los datos que se presenta. A esta figura se le asigna un valor en las unidades que esta
representa y se repite tantas veces en le gráfico hasta alcanzar la magnitud del fenómeno.
Al confeccionar estos gráficos se deben tener en cuenta que las cantidades mayores se
indican por un número mayor de símbolos no por símbolos más grandes.
Tablas y Gráficos Estadísticos
Tablas
Las tablas estadísticas aparecen por todas partes y consisten en masas
estructuradas de datos. Con frecuencia su aspecto es temible y al no experto le
producen la sensación de que poco o nada podrá sacar en claro de ellas. Sin
embargo si se las mira con fe se puede apreciar que no sólo no es difícil, sino que es
muy fácil leer en ellas.
Pero si además de con fe, se las mira con un poco de conocimiento, los datos
cobran vida y dirán mucho más de lo que puede aparecer a primera vista.
Dispersograma
Los Dispersogramas son gráficos que se construyen sobre dos ejes ortogonales de coordenadas, llamados cartesianos, cada punto corresponde a un par de valores de datos x e y de un mismo elemento suceso.
Histogramas
Los Histogramas son tipos de gráficos que se utilizan para representa distribuciones de frecuencias. Algún software específico para estadística grafican la curva de gauss superpuesta con el histograma.
Gráficos de áreas
En los Gráficos de Áreas se busca mostrar la tendencia de la información generalmente en un período de tiempo. Pueden utilizarse para representar una o más series y en dos dimensiones o en tres dimensiones
Cartogramas
Los Cartogramas se utilizan para mostrar datos sobre una base geográfica. La densidad de datos se puede marcar por círculos, sombreado, rayado o color.
Gráficos mixtos
Los Gráficos Mixtos representan dos o más series de datos, cada una con un tipo diferente de gráfico. Son gráficos más vistosos y se usan para resaltar las diferencias entre las series. Pueden presentarse en dos o en tres dimensiones.
Las tablas estadísticas están confeccionadas de tal modo que resultan muy
fáciles de leer y de interpretar. Utiliza fundamentalmente el sentido común.
Las tablas estadísticas tienen mucha más información que la que aparece a
primera vista. Para obtenerla conviene relacionar unas líneas con otras,
operar con ellas, obtener conclusiones adicionales. Para ello se debe recurrir
con frecuencia a la interpretación como porcentajes de uno datos respecto de
otros.
En todas las tablas suele haber redundancias, es decir, se da información que
podía haberse obtenido por otro conducto dentro de la misma tabla. Esto es
lógico, pues la misión de una tabla no es sólo dar información, sino facilitar la
lectura de la misma.
Es muy frecuente, que las tablas que vienen en diarios, revistas, libros de
divulgación, folletos informativos, etc., tengan errores. (hasta tal punto que
estamos tentados a dar una regla que diga: toda tabla tiene errores, con la
convicción de que la regla tendrá muy pocas excepciones). Las redundancias
permiten descubrirlos. También el sentido común y nuestros conocimientos
previos nos alertan, a veces, sobre datos chocantes: en tal caso recurre a
otras fuentes.
Estadística Descriptiva
La estadística descriptiva es una gran parte de la estadística que se dedica a recolectar, ordenar, analizar y representar a un conjunto de datos, con el fin de describir apropiadamente las características de este.
A partir del siglo XIX , entre otros, con el aporte de Adolphe Quetelet (1796-1874), se crearon diferentes métodos de cálculo de probabilidades para determinar y analizar el tipo de datos que regulan algunos fenómenos.
Media Aritmética: Se obtiene a partir de la suma de todos sus valores dividida entre el número de sumados.
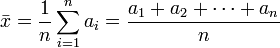
Se utiliza la letra X con una barra horizontal sobre el símbolo para representar la media de una muestra ( ), mientras que la letra µ (mu) se usa para la media aritmética de una población, es decir, el valor esperado de una variable.
), mientras que la letra µ (mu) se usa para la media aritmética de una población, es decir, el valor esperado de una variable.
 ), mientras que la letra µ (mu) se usa para la media aritmética de una población, es decir, el valor esperado de una variable.
), mientras que la letra µ (mu) se usa para la media aritmética de una población, es decir, el valor esperado de una variable.
En otras palabras, es la suma de n valores de la variable y luego dividido por n : donde n es el número de sumados, o en el caso de estadística el número de datos se da el resultado.
Mediana(Estadística): representa el valor de la variable de posición central en un conjunto de datos ordenados.
Existen dos métodos para el cálculo de la mediana:
- Considerando los datos en forma individual, sin agruparlos.
- Utilizando los datos agrupados en intervalos de clase.
Datos sin agrupar
Sean 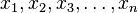 los datos de una muestra ordenada en orden creciente y designando la mediana como
los datos de una muestra ordenada en orden creciente y designando la mediana como 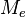 , distinguimos dos casos:
, distinguimos dos casos:
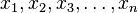 los datos de una muestra ordenada en orden creciente y designando la mediana como
los datos de una muestra ordenada en orden creciente y designando la mediana como 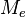 , distinguimos dos casos:
, distinguimos dos casos:a) Si n es impar, la mediana es el valor que ocupa la posición
 una vez que los datos han sido ordenados (en orden creciente o decreciente), porque éste es el valor central.
una vez que los datos han sido ordenados (en orden creciente o decreciente), porque éste es el valor central.
b) Si n es par, la mediana es la media aritmética de los dos valores centrales. Cuando  es par, los dos datos que están en el centro de la muestra ocupan las posiciones
es par, los dos datos que están en el centro de la muestra ocupan las posiciones  y
y 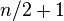 . Es decir:
. Es decir: 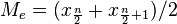 .
.
 es par, los dos datos que están en el centro de la muestra ocupan las posiciones
es par, los dos datos que están en el centro de la muestra ocupan las posiciones  y
y 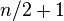 . Es decir:
. Es decir: 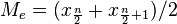 .
.Datos agrupados
Al tratar con datos agrupados, si 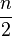 coincide con el valor de una frecuencia acumulada, el valor de la mediana coincidirá con la abscisa correspondiente. Si no coincide con el valor de ninguna abscisa, se calcula a través de semejanza de triángulos en el histograma o polígono de frecuencias acumuladas.
coincide con el valor de una frecuencia acumulada, el valor de la mediana coincidirá con la abscisa correspondiente. Si no coincide con el valor de ninguna abscisa, se calcula a través de semejanza de triángulos en el histograma o polígono de frecuencias acumuladas.
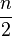 coincide con el valor de una frecuencia acumulada, el valor de la mediana coincidirá con la abscisa correspondiente. Si no coincide con el valor de ninguna abscisa, se calcula a través de semejanza de triángulos en el histograma o polígono de frecuencias acumuladas.
coincide con el valor de una frecuencia acumulada, el valor de la mediana coincidirá con la abscisa correspondiente. Si no coincide con el valor de ninguna abscisa, se calcula a través de semejanza de triángulos en el histograma o polígono de frecuencias acumuladas.
EJEMPLO:
| xi | fi | Ni |
|---|---|---|
| 1 | 2 | 2 |
| 2 | 2 | 4 |
| 3 | 4 | 8 |
| 4 | 5 | 13 |
| 5 | 8 | 21 > 19.5 |
| 6 | 9 | 30 |
| 7 | 3 | 33 |
| 8 | 4 | 37 |
| 9 | 2 | 39 |
Las calificaciones en la asignatura de Matemáticas de 39 alumnos de una clase viene dada por la siguiente tabla:
| Calificaciones | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| Número de alumnos | 2 | 2 | 4 | 5 | 8 | 9 | 3 | 4 | 2 |
Primero se hallan las frecuencias absolutas acumuladas  . Así, aplicando la fórmula asociada a la mediana para n impar, se obtiene
. Así, aplicando la fórmula asociada a la mediana para n impar, se obtiene 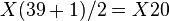 .
.
 . Así, aplicando la fórmula asociada a la mediana para n impar, se obtiene
. Así, aplicando la fórmula asociada a la mediana para n impar, se obtiene 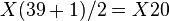 .
.- Ni-1< n/2 < Ni = N19 < 19.5 < N20
Por tanto la mediana será el valor de la variable que ocupe el vigésimo lugar.En este ejemplo, 21 (frecuencia absoluta acumulada para Xi = 5) > 19.5 con lo que Me = 5 puntos, la mitad de la clase ha obtenido un 5 o menos, y la otra mitad un 5 o más.
Moda(Estadística):La moda es el valor con una mayor frecuencia en una distribución de datos.
Se hablará de una distribución bimodal de los datos adquiridos en una columna cuando encontremos dos modas, es decir, dos datos que tengan la misma frecuencia absoluta máxima. Una distribución trimodal de los datos es en la que encontramos tres modas. Si todas las variables tienen la misma frecuencia diremos que no hay moda.
El intervalo moanolo es el de mayor frecuencia absoluta. Cuando tratamos con datos agrupados antes de definir la moda, se ha de definir el intervalo modal.
La moda, cuando los datos están agrupados, es un punto que divide al intervalo modal en dos partes de la forma p y c-p, siendo c la amplitud del intervalo, que verifiquen que:

















